Problem statement

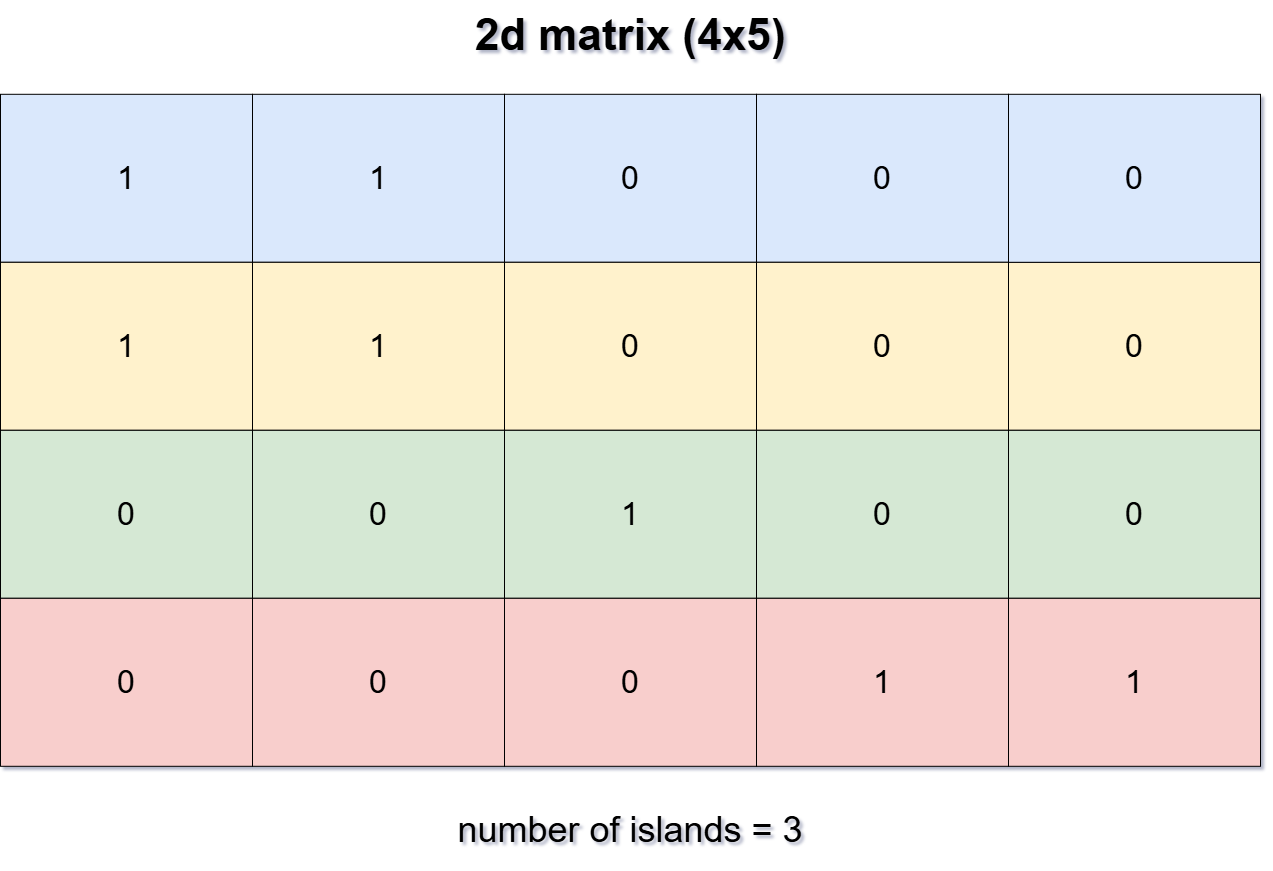
Given an m x n 2D binary grid which represents a map of ‘1’s (land) and ‘0’s (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent land cells horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] is '0' or '1'.

Solution

To solve this problem we need to loop through the two-dimensional array, and perform a Breadth-First Search on each land, increasing the number of islands counter. In the BFS we are going to search and mark as visited all the adjacent nodes, vertically or horizontally so they can be considered as part of the same island. Once there are no more adjacent land cells, start again until we have traversed the entire grid. As usual, it can be resolved iteratively or recursively. In this post we are going to focus on the iterative version.

Introduction

We will need:

• A queue to store the indices (row and column) as a number that we are going to visit using the BFS algorithm
• An integer to represent the counter of the number of islands

Step 1

Loop through each element of the array starting from i=0, j=0

Step 2

If we find a ‘1’ land:

• Increment number of islands counter
• Mark as visited by modifying the grid value to water ‘0’
• Enqueue the current node index by the formula row * NUMBER_OF_COLUMNS + column. We will parse this index later like this:
  • row: Math.floor(index / NUMBER_OF_COLUMNS)
  • column: index % NUMBER_OF_COLUMNS

Step 3

If the queue is not empty, perform a Breadth-First Search

1. Search adjacent nodes in all four directions (bottom, right, left, top):

• Right: (row, column + 1)
• Bottom: (row + 1, column)
• Left: (row, column - 1)
• Top: (row - 1, column)

For each adjacent node:

• Verify it’s within grid boundaries
• Verify it’s land (‘1’), not water (‘0’)

2. If we detect land ‘1’, mark as visited by changing the value to water ‘0’ and enqueue this node index

3. At the end of the iteration, dequeue the head

Run BFS iteratively, adding the index to the queue and marking as visited until the queue is empty, with this approach we will mark all the adjacent land cells as visited for the current island. Once we finish the BFS, we go back to step 1 and continue traversing the grid until we find another land ‘1’ to start a new island count.

Code

import { Queue } from '../queue';

/*
  Assume that you have a Queue like this one:

  export interface Queue<T> {

      constructor(maxSizeOfQueue: number)

      enqueue(value: T): boolean

      dequeue(): boolean

      front(): T | null

      rear(): T | null

      isEmpty(): boolean

      isFull(): boolean

      size(): number
  }
 */

export function numIslands(grid: string[][]): number {
  // introduction
  const ROWS = grid.length;
  if (ROWS === 0) {
    return 0;
  }
  const COLUMNS = grid[0].length;

  const queue = new Queue<number>(COLUMNS * ROWS);
  let numberOfIslands = 0;

  // step 1: loop through the matrix
  for (let i = 0; i < ROWS; i++) {
    for (let j = 0; j < COLUMNS; j++) {
      // step 2: find '1's lands
      const currentValue = grid[i][j];

      if (currentValue !== '1') continue;

      numberOfIslands++;
      queue.enqueue(i * COLUMNS + j);
      grid[i][j] = '0';

      const fill = (row: number, column: number) => {
        if (
          row >= ROWS ||
          column >= COLUMNS ||
          row < 0 ||
          column < 0 ||
          grid[row][column] === '0'
        ) {
          return;
        }

        queue.enqueue(row * COLUMNS + column);
        grid[row][column] = '0';
      };

      // step 3: BFS algorithm
      while (!queue.isEmpty()) {
        const node = queue.front()!;
        const row = Math.floor(node / COLUMNS);
        const column = node % COLUMNS;

        // search adjacent nodes
        fill(row, column + 1); // right
        fill(row + 1, column); // bottom
        fill(row, column - 1); // left
        fill(row - 1, column); // top

        queue.dequeue();
      }
    }
  }

  return numberOfIslands;
}

Complexity analysis

• Time complexity: O(n), where n is the rows * columns, so the number of cells in the grid
• Space complexity: O(n), where n is the number of cells in the grid